
PhD Thesis
Abstract¶
Inverse modeling is a powerful tool for extracting information about the subsurface from geophysical and hydrologic data. Geophysical inverse problems are inherently multidisciplinary, requiring elements from the relevant physics, numerical simulation, and optimization, as well as knowledge of the geologic setting, hydrologic processes, and a comprehension of the interplay between all of these elements. Increasingly geoscientists are tackling complex problems that require integration of multiple types of information in order to better characterize the subsurface. However, many of the sub-fields of geophysics are developing simulation and inversion approaches, algorithms, and supporting software in isolation. This isolation is a barrier to quantitative integration and leads to inefficiencies in advancing interdisciplinary research. Greater efficiencies, and higher quality outcomes, could be achieved if (hydro)geophysicists had a common framework to accelerate an integrated approach. The main goal of my thesis is to organize the components of (hydro)geophysical simulations and inverse problems, and synthesize these into a comprehensive, modular framework.
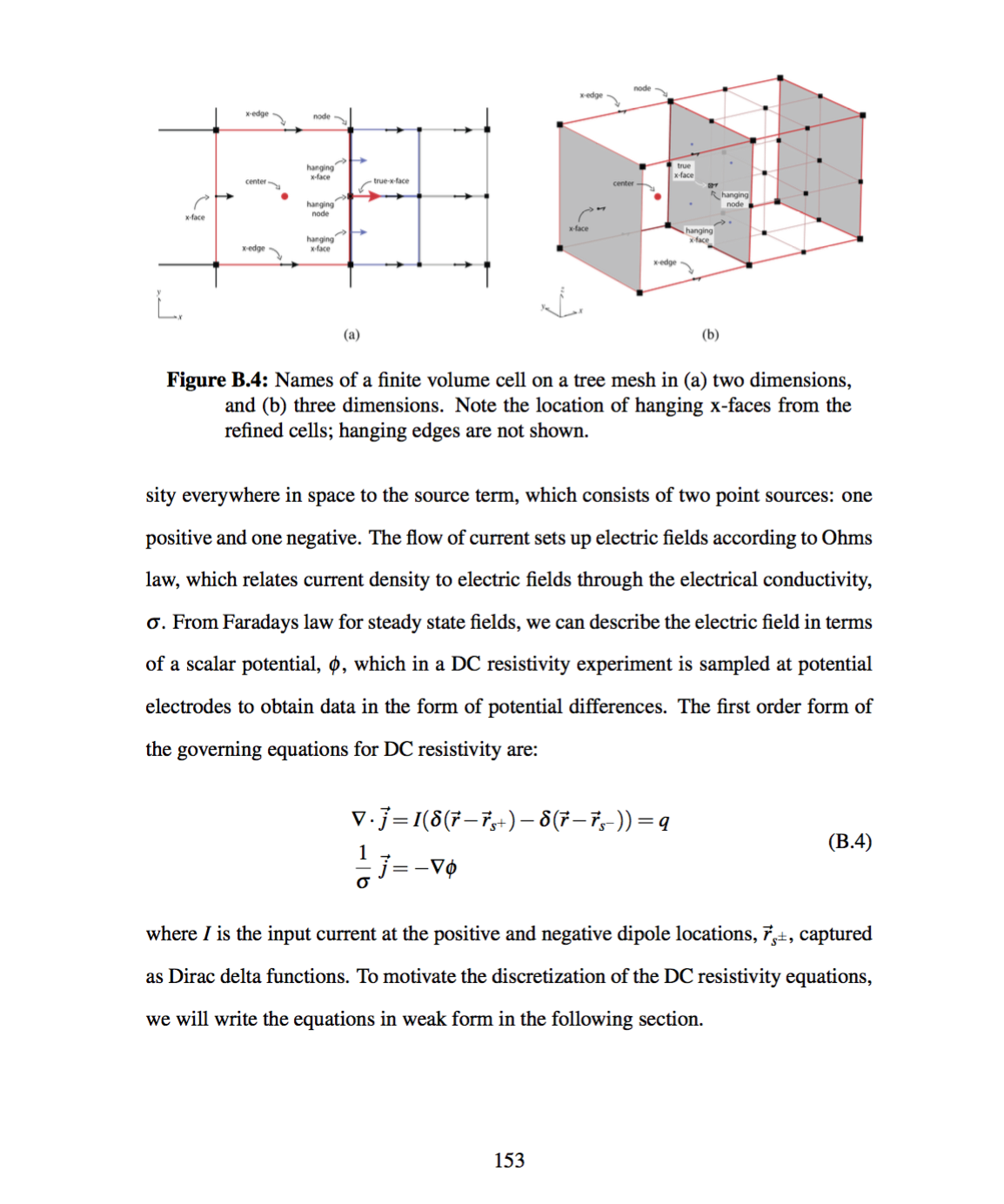
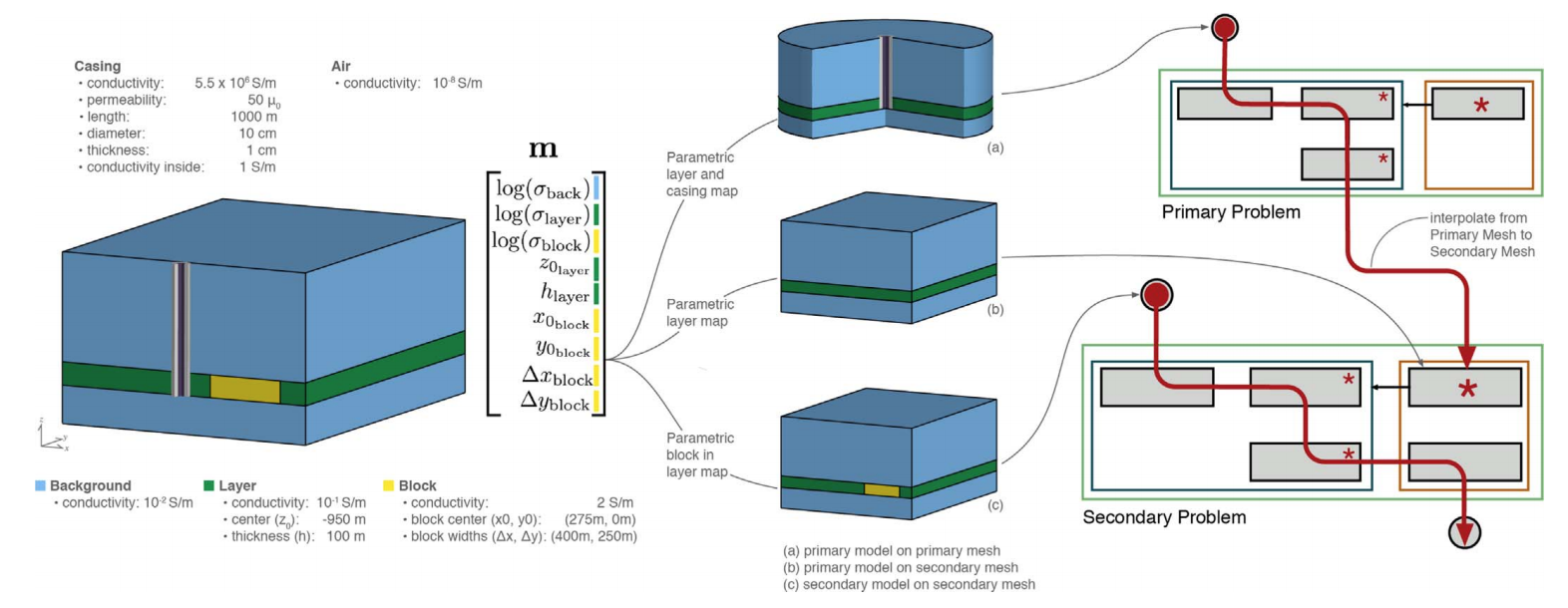
The development of a geophysical framework requires considering a number of disciplines and geophysical problems (e.g. electromagnetics and potential fields) to ensure generality as well as extensibility. However, the goal is also to have the framework work outside of geophysics and most notably in hydrogeology; vadose zone fluid flow is used as a model problem. Fluid flow in the vadose zone is governed by the Richards equation; it is parameterized by hydraulic conductivity, which is a nonlinear function of pressure head. The computational scalability of the Richards equation inversion is a significant challenge for three dimensional inversions in hydrogeophysics. Existing work explicitly calculates the sensitivity matrix using finite difference or automatic differentiation, however, for large-scale problems these methods are constrained by computation and memory. This dissertation provides an implicit sensitivity algorithm that enables large-scale inversion problems for distributed parameters in the Richards equation to become tractable on modest computational resources.
Full Thesis¶
A framework for geophysical inversions with application to vadose zone parameter estimation. Read more.
Contributions¶
a conceptual organization and synthesis of geophysical simulations and inversions into a framework that has been rigorously, numerically tested; and
an algorithm for large-scale vadose zone parameter estimation for any distributed hydraulic parameter, regardless of the empirical relationship used.
One outcome of a framework approach is the accelerated transfer of ideas from one discipline to another. For example, the implicit sensitivity calculation for the Richards equation was heavily inspired by research completed in time-domain electromagnetics simulations and inversions. The refinement and application of this algorithm to hydrology significantly improved numerical scalability for the 3D inverse problem. Chapter 4 showed significant improvements in memory over explicitly forming the sensitivity matrix by over two orders of magnitude for the example shown, bringing this inversion into the range of possibility on modest computational resources. Additionally, the complexities of the Richards equation were generalized and synthesized to improve other geophysical methods in the framework. These improvements were especially demonstrated with regard to dealing with multiple physical properties that may or may not be estimated and occur in distributed empirical relations throughout the forward simulation framework.
Outlook¶
This thesis is positioned from a perspective of looking out to a future of multidisciplinary, multi-data-type, quantitatively integrated geoscience simulations and inversions. A future where joint, cooperative, coupled, parameterized, multiphysics inversions and simulations are the norm rather than the exception. Where multiple existing, robust, and computationally-efficient methodologies are combined to extract all possible information from disparate geoscience datasets. To realize this sort of ubiquitous, quantitative communication between disciplines and methodologies requires an organized and integrated community that can effectively work together. My research is aimed here. This future will not be realized by one person nor by one research group. In the field of machine learning, Olah & Carter (2017) note that “[t]he maintainable size of the field is controlled by how its members trade off the energy between communicating and understanding.” The curation of ideas is just as important as their creation. There is a research debt created by an exclusive focus on research novelty; future advances also require distillation, synthesis, and explicit communication. There is a significant amount of effort ahead of us to achieve effective communication and collaboration with our geoscience peers in geology and hydrogeology. This communication and quantitative integration is the webbing on which the future of our geoscience field depends. My approach, therefore, has been to research and disseminate a numerical framework that attempts to support and enable a number of these diverse interdisciplinary collaborations. I hope that a lasting contribution of my work is the open, modular approach that I have curated and the community that I have helped to seed around these ideas.
Reflecting on creating tools for technical communication.
UCalgary Geosicence - Friday Afternoon Talk Series

Podcast with Matt Hall and Graham Ganssle

A framework for geophysical inversions
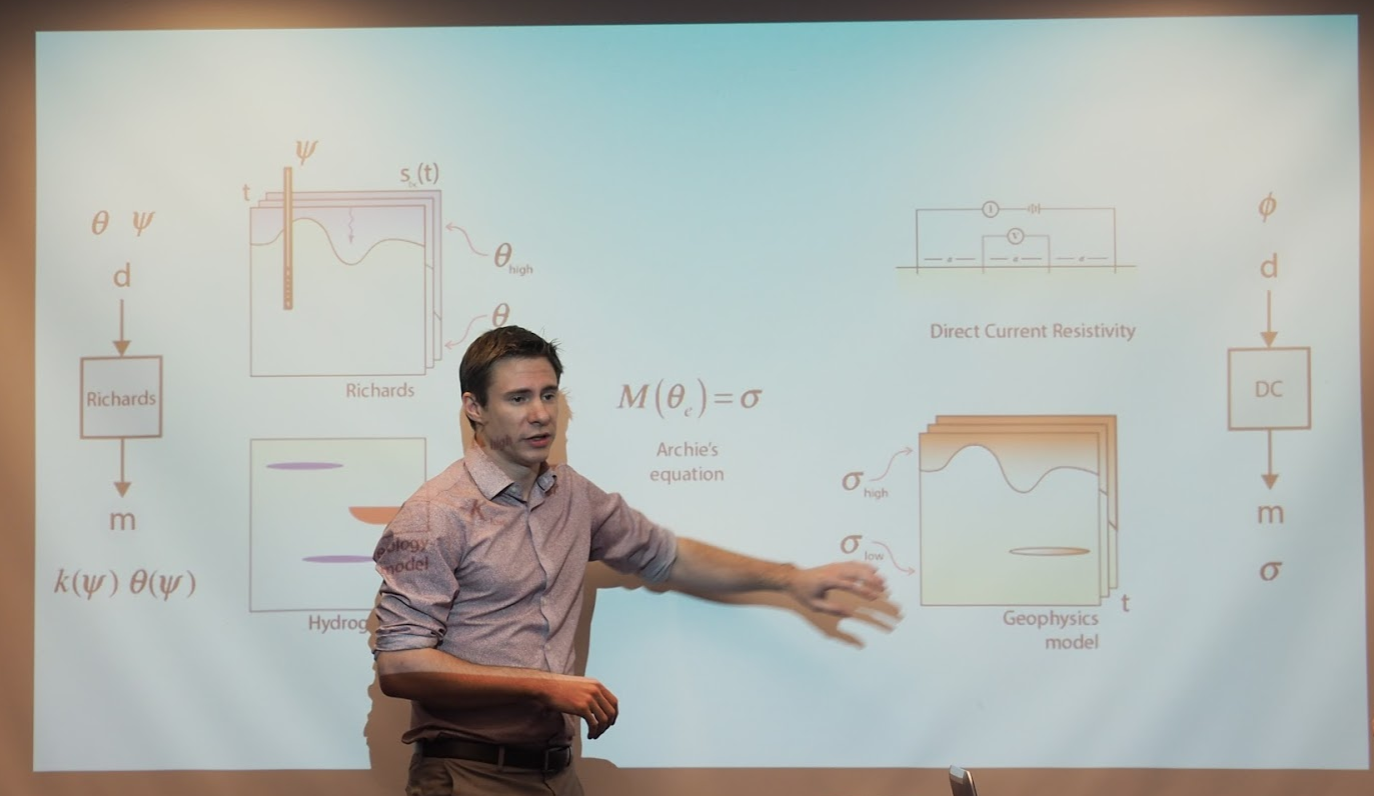
My PhD Defence
A framework for simulation and inversion in electromagnetics