Logically Rectangular Meshes
for EM applications
Rowan Cockett & Eldad Haber, April 2013
Overview
Cells have the same number of neighbors as a regular mesh.
Tensor Mesh
Logically Rectangular Mesh
Topography
- Align mesh to features
- Reduce number of cells
- Increase modelling accuracy
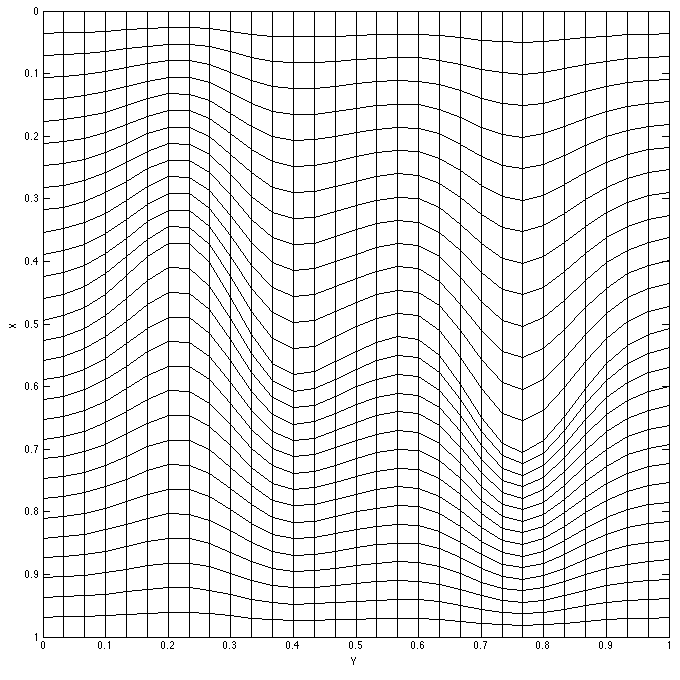
Infinity
- Maintain a better aspect ratio for padding cells
- Equal radius to 'infinity'
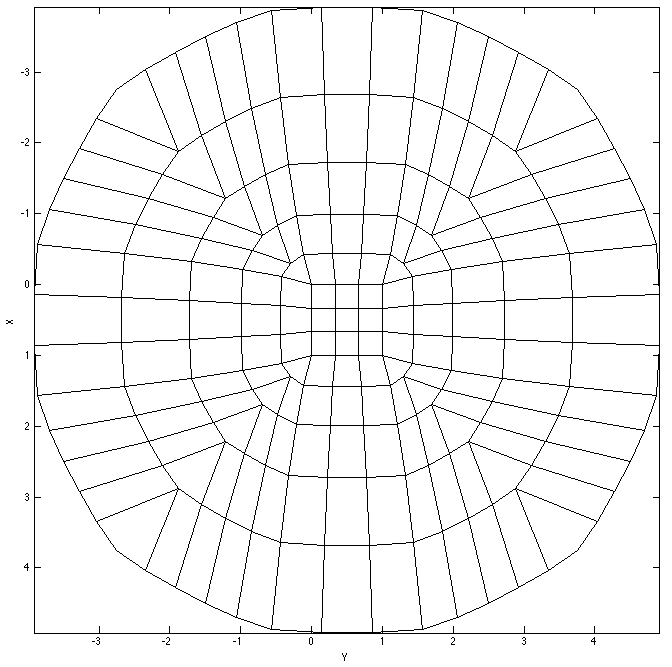
DC Resistivity Equations
$$ \begin{align} \nabla \cdot \mathbf{J} &= \mathbf{q}\\ \sigma^{-1} \mathbf{J} &= -\nabla \mathbf{\phi}\\ \end{align} $$
First equation, define geometrically:
$$ \int_V \nabla \cdot \mathbf{J} \;dV = \oint_{\partial V} (\mathbf{J},\vec{n}) \; dS $$
Discretize over a single cell:
$$ \text{DIV} \mathbf{J}_{\text{cell}} = V^{-1}(J_{\text{cell}}^{\text{in}} A - J_{\text{cell}}^{\text{out}} A) $$
Divergence Over a Cell
For a single cell, calculate surface areas and volumes:
$$ \text{DIV} \mathbf{J}_{\text{cell}} = V^{-1}(J^{(1)} A^{(1)} - J^{(2)} A^{(2)} + J^{(3)} A^{(3)} - J^{(4)} A^{(4)} ) $$
getDivergence3D
function [DIV] = getDivergence3D(h, n)
ddx = @(n)(spdiags(ones(n+1,1)*[-1,1],[0,1],n,n+1));
A = cellArea(h);
V = cellVol(h);
Dx = kron(speye(n(3)),kron(speye(n(2)),ddx(n(1))));
Dy = kron(speye(n(3)),kron(ddx(n(2)),speye(n(1))));
Dz = kron(ddx(n(3)),kron(speye(n(2)),speye(n(1))));
DIV = sdiag(1./V) * [Dx,Dy,Dz] * sdiag(A);
end
DC Resistivity Equations
$$ \begin{align} \nabla \cdot \mathbf{J} &= \mathbf{q}\\ \sigma^{-1} \mathbf{J} &= \nabla \mathbf{\phi}\\ \end{align} $$
Regular approach to second equation:
- Break into parts and integrate over x and y
- Rectangle rule integration over the cell
Weak Form Definition
$$ \sigma^{-1} \mathbf{J} = \nabla \mathbf{\phi} $$
So, define in weak form by integrating with a general face function \(\mathbf{F}\)
$$ \int_{\text{cell}} {\sigma^{-1} \mathbf{J} \cdot \mathbf{F} } = \int_{\text{cell}} {\nabla \phi \cdot \mathbf{F} } $$
$$ \int_{\text{cell}} {\sigma^{-1} \mathbf{J} \cdot \mathbf{F} } = -\int_{\text{cell}} {(\nabla \cdot \mathbf{F})\phi } + \int_{\partial \text{cell}} {\phi \mathbf{F} \cdot \mathbf{n}} $$
$$ v_{\text{cell}} \sigma^{-1} (\mathbf{J}_x \mathbf{F}_x +\mathbf{J}_y \mathbf{F}_y ) = -\phi^{\top} v_{\text{cell}} (\text{DIV}_{\text{cell}} \mathbf{F}) + \text{BC} $$
We need \(\mathbf{J}_x\) and \(\mathbf{J}_x\)
Face Inner Product
$$\left[\begin{smallmatrix}J^{(1)} \\J^{(3)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(1)}_x & n^{(1)}_y \\n^{(3)}_x & n^{(3)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$\left[\begin{smallmatrix}J^{(1)} \\J^{(4)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(1)}_x & n^{(1)}_y \\n^{(4)}_x & n^{(4)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$\left[\begin{smallmatrix}J^{(2)} \\J^{(3)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(2)}_x & n^{(2)}_y \\n^{(3)}_x & n^{(3)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$\left[\begin{smallmatrix}J^{(2)} \\J^{(4)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(2)}_x & n^{(2)}_y \\n^{(4)}_x & n^{(4)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$\mathbf{J}_c = \mathbf{N}_{(i)}^{-1}\mathbf{P}_{(i)}\mathbf{J}$
Face Inner Product
Sub in for the cartesian face functions, $\mathbf{J}_c = \mathbf{N}_{(i)}^{-1}\mathbf{P}_{(i)}\mathbf{J}$
$$
\mathbf{F}_c^{\top} (v_{\text{cell}} \sigma^{-1}) \mathbf{J}_c
=
-\phi^{\top} v_{\text{cell}}( v_\text{cell}^{-1} \mathbf{D}_{\text{cell}} \mathbf{A} \mathbf{F}) + \text{BC}
$$
$$
\mathbf{F}^{\top}
{1\over 4}
\left(\sum_{i=1}^4
\mathbf{P}_{(i)}^\top \mathbf{N}_{(i)}^{-\top} v_{\text{cell}} \sigma^{-1} \mathbf{N}_{(i)}^{-1}\mathbf{P}_{(i)}
\right)
\mathbf{J}
=
-\mathbf{F}^{\top} \mathbf{A} \mathbf{D}_{\text{cell}}^{\top} \phi + \text{BC}
$$
So for any discretized face function:
$$ \mathbf{M}(\sigma^{-1}) \mathbf{J} = -\mathbf{A} \mathbf{D}_{\text{cell}}^{\top} \phi + \text{BC} $$
$$\mathbf{M}(\sigma^{-1}) = {1\over 4} \left(\sum_{i=1}^4 \mathbf{P}_{(i)}^\top \mathbf{N}_{(i)}^{-\top} v_{\text{cell}} \sigma^{-1} \mathbf{N}_{(i)}^{-1}\mathbf{P}_{(i)} \right)$$
Need to create for all cells - projection matrices!
ave((x)^2) vs (ave(x))^2
$$\left[\begin{smallmatrix}J^{(1)} \\J^{(3)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(1)}_x & n^{(1)}_y \\n^{(3)}_x & n^{(3)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$\left[\begin{smallmatrix}J^{(1)} \\J^{(4)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(1)}_x & n^{(1)}_y \\n^{(4)}_x & n^{(4)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$\left[\begin{smallmatrix}J^{(2)} \\J^{(3)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(2)}_x & n^{(2)}_y \\n^{(3)}_x & n^{(3)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$\left[\begin{smallmatrix}J^{(2)} \\J^{(4)} \\\end{smallmatrix}\right]=\left[\begin{smallmatrix}n^{(2)}_x & n^{(2)}_y \\n^{(4)}_x & n^{(4)}_y \\\end{smallmatrix}\right]\left[\begin{smallmatrix}J_x \\J_y \\\end{smallmatrix}\right]$$
$$ \left[\begin{smallmatrix} J^{(1)} \\ J^{(2)} \\ J^{(3)} \\ J^{(4)} \\ \end{smallmatrix}\right] = \left[\begin{smallmatrix} n^{(1)}_x & n^{(1)}_y \\ n^{(2)}_x & n^{(2)}_y \\ n^{(3)}_x & n^{(3)}_y \\ n^{(4)}_x & n^{(4)}_y \\ \end{smallmatrix}\right] \left[\begin{smallmatrix} J_x \\ J_y \\ \end{smallmatrix}\right] $$
$$\mathbf{M}(\sigma^{-1}) = {1\over 4} \left(\sum_{i=1}^4 \mathbf{P}_{(i)}^\top \mathbf{N}_{(i)}^{-\top} v_{\text{cell}} \sigma^{-1} \mathbf{N}_{(i)}^{-1}\mathbf{P}_{(i)} \right)$$
or$$\mathbf{M}(\sigma^{-1}) = \mathbf{N}^{\dagger^\top} \mathbf{V}_{\text{cell}} \sigma^{-1} \mathbf{N}^{\dagger} $$
Need to make \(\mathbf{M}(\sigma^{-1})\) invertable!
$$(-1 + 1)^2 = 0$$
Moving to 3D
- 8 inner product matricies to average
- Edge inner products needed as well (for \(\nabla \times\))
- Volume and face areas may not be well defined
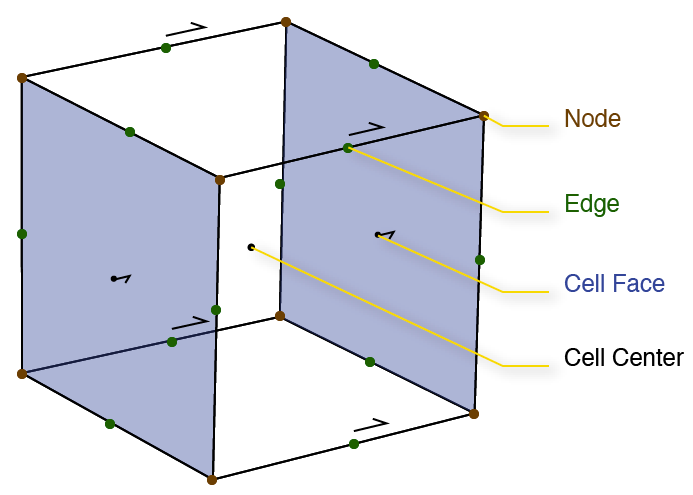
DC Resistivity System
Combine equations into a matrix system:
$$\left[\begin{smallmatrix} \mathbf{M}(\sigma^{-1}) & - \text{diag}(\mathbf{a}) \mathbf{D}^\top \\ -\mathbf{D} \text{diag}(\mathbf{a}) & 0 \\ \end{smallmatrix}\right] \left[\begin{smallmatrix} j \\ \phi \\ \end{smallmatrix}\right] = \left[\begin{smallmatrix} 0 \\ -\text{diag}(\mathbf{v}) s \\ \end{smallmatrix}\right] $$
Solve for \(\phi\) using (smart!) iterative methods.
Example: Align mesh to layer
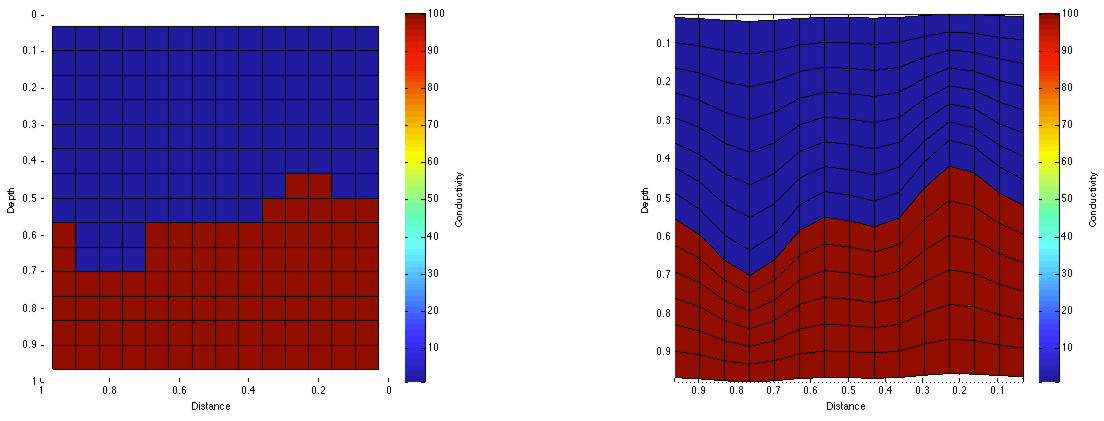 Use same number of cells and compare to finely discretized model.
Use same number of cells and compare to finely discretized model.
Results
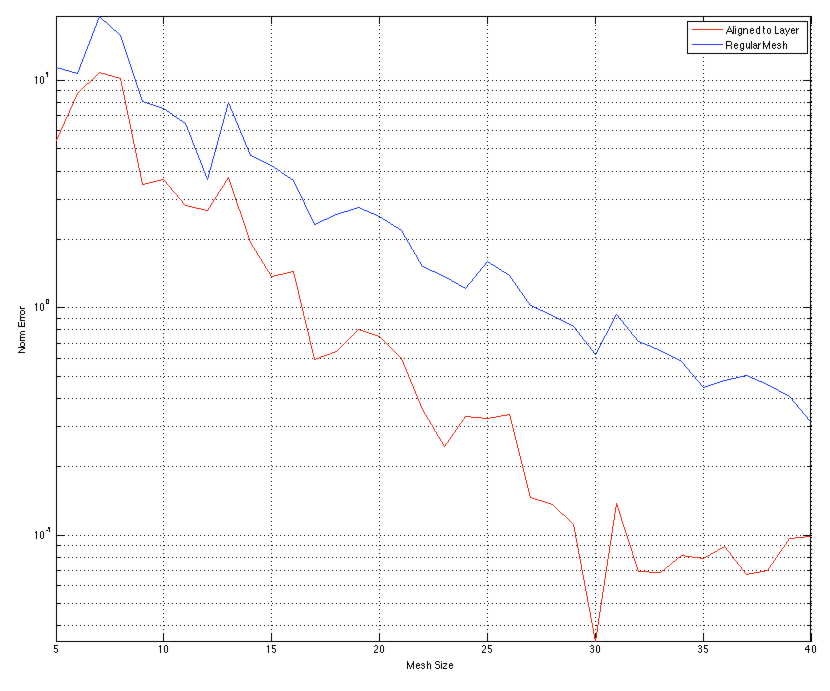
Preliminary Conclusions
- Handling known interfaces (e.g. topography)
- Padding to infinity